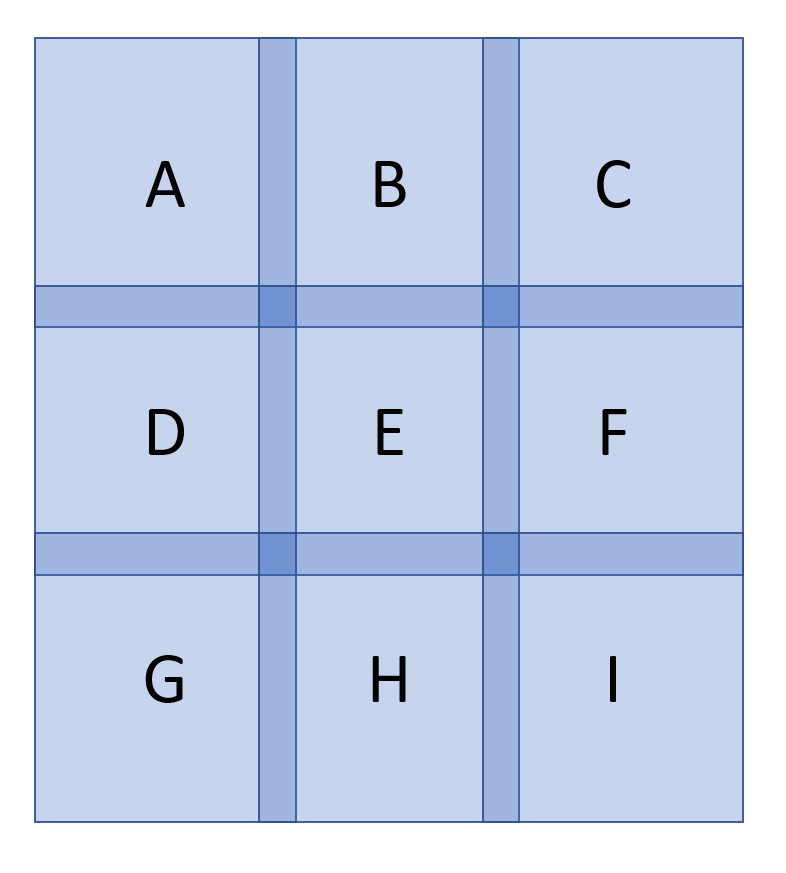
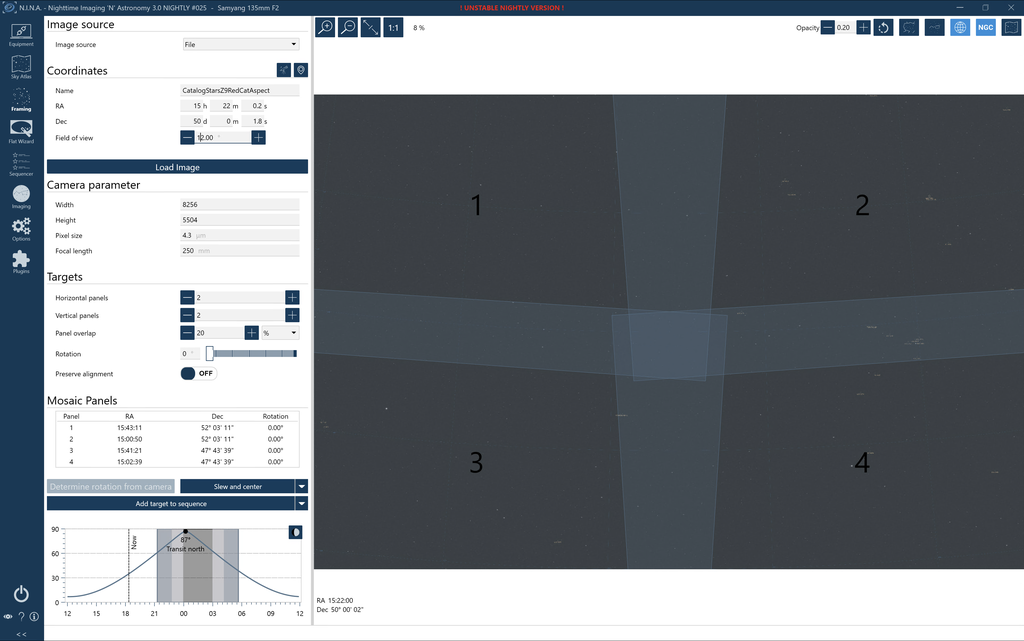
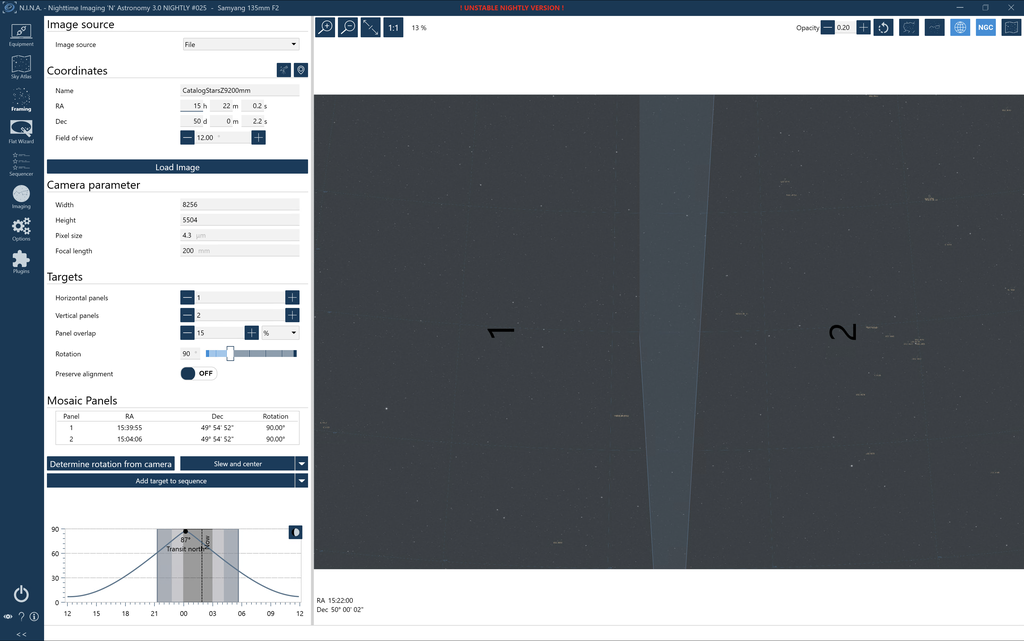
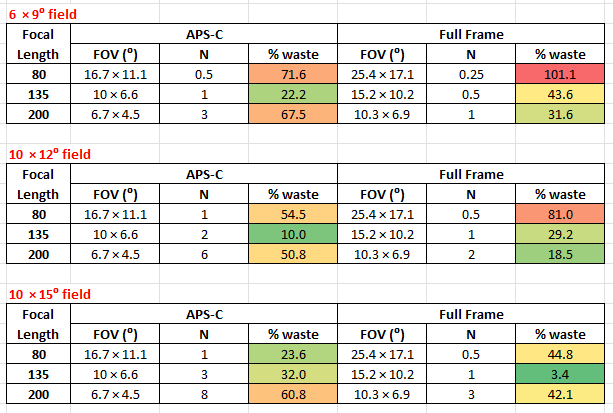
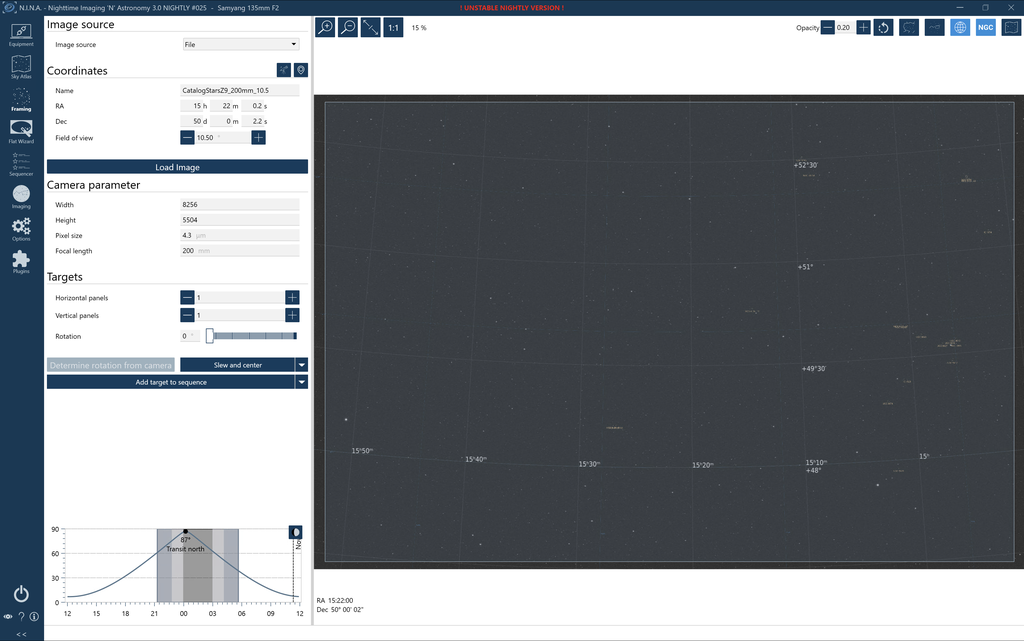
Consider a section of a mosaic shown below, where each lettered region is a 12 x 12 degree field and the darker blue regions are the overlaps. Let us imagine that the fields have been submitted by different users - they have been 'undistorted' using AlignByCoordinates or a similar PI script, and that the user has made their best efforts to remove gradients.
Suppose that we are trying to work on the central field 'E'. Where we have overlaps with the surrounding fields A, B, C etc we calculate the average RGB value for all overlapping images (including the contribution from E itself). Where there is no overlap in the centre of field E we assign a null value. The difference between the RGB values of field E and the average valuesjust calculated provides an estimate of the unwanted gradient of image E in the overlap region. Probably to avoid problems with different star shapes, misaligned stars etc we would remove the stars from all of the images before performing the maths.
We now interpolate this residual gradient value across the centre of tile E. Finally we can subtract the residual gradient to obtain the 'true' image for field E. Repeating this procedure across the grid allows us to make the corrections for the entire sky.
Some comments:
- By construction, the algorithm should eliminate or at least minimise seams between images. Effectively each overlapping image is corrected to have the same RGB values on a scale governed by the interpolation algorithm.
- Whilst the algoithm cannot of course estimate the 'true' gradient perfectly, it makes a best estimate by averaging across the available data taken (presumably) by different observers at different times, maybe using different equipment.
- The algorithm should provide a quantitative approach to QC: any field whose RGB values in the overlap region differ too much is suspect and should be reviewed.