1.91
...
·
 |
|---|
In PI, can I separate the OIII, HA and SII channels from the Antlia Quadband? Will DB Extract do this? Any insight would be appreciated.
|
19.44
...
·
·
3
likes
|
|---|
This is impossible. Unfortunately, companies like to market these filters as though it is, or it somehow provides some benefit, but data captured with this filter cannot be decomposed into its component emission lines. You would need two sets of different filters to extract Ha, Sii and Oiii. Something like the Askar D1 + D2 would be your only real option for achieving SHO with an OSC camera. It cannot be done in one filter as Ha and Sii are both recorded as Red with a one shot color camera. |
5.94
...
·
|
|---|
I agree with above. You have recored RGB data, and that is what your left with. You can saperate into Red, Green & Bue. You can treat the red as Ha, but it will also include some SII. You can combine the Green & Blue to get synthetic OIII. But it will not be true OIII. What you want to do requires a Mono camera and individual filters. Lynn K. |
|
1.91
...
·
|
|---|
Thanks for the info everyone. Someday I will get a mono camera and filters.
|
0.00
...
·
|
|---|
You can use a colour camera as Charles said using dual band filers. I use antlia alp-t ha+oiii, sii+hb filters and uvir cut for coloured stars. Seems to work quite well
|
7.22
...
·
·
1
like
|
|---|
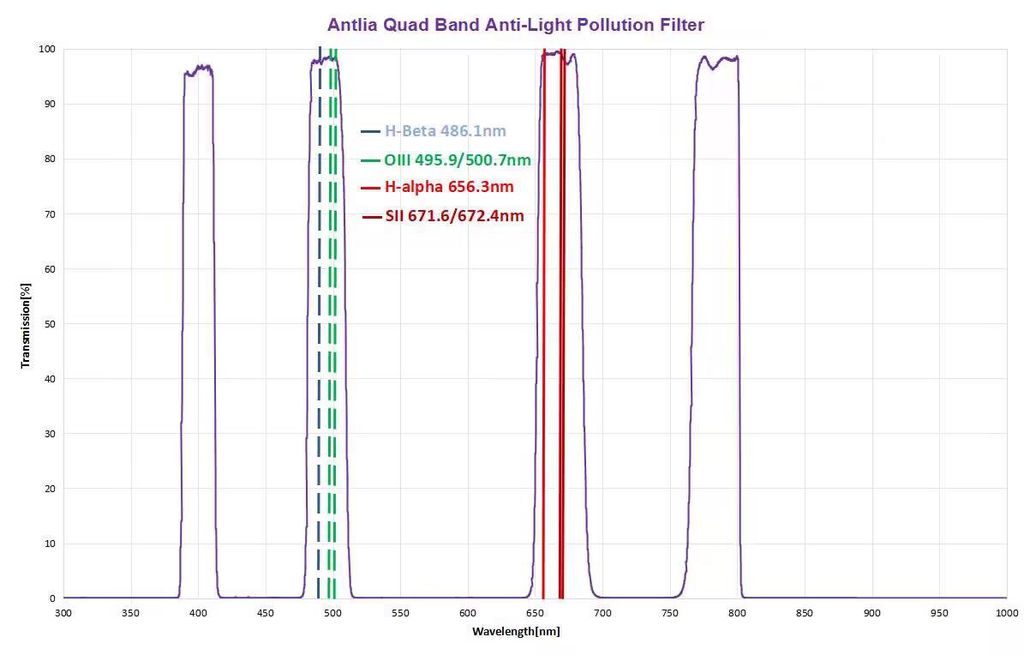
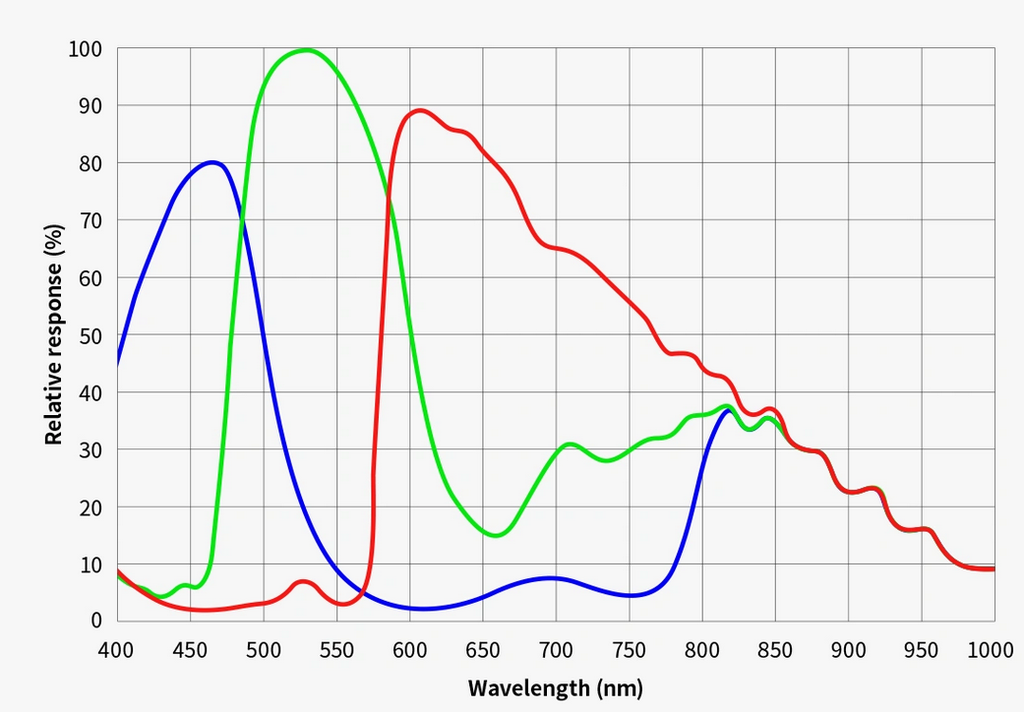
Strictly speaking from a Linear Algebra perspective, it should be perfectly doable. You'd need to overlap the filter's transmission graph on top of the camera's QE curves: From antliafilter.com  From zwoastro.com (2600MC PRO):  The camera provides three independent channels (RGB) and you want to extract three band-passes. It would be a matter of picking some values for the 9 constants below (*): Ha = h1*R+h2*G+h3*B OIII = o1*R+o2*G+o3*B SII = s1*R+s2*G+s3*B It shouldn't be much different to the usual methods to extract NB channels from dual-band filters coupled with OSC cameras. I've never done such calculations myself, but someone like @Franklin Marek might find it a good challenge to follow... (*) Edit: The h1,h2,h3,o1,o2,o3,s1,s2,s3 constants could also be obtained by inverting the matrix R = r1*H + r2*O + r3*S G = g1*H + g2*O + g3*S B = b1*H + b2*O + b3*S As mentioned, from a Linear Algebra perspective seems perfectly doable, the dimensions add up. |
7.29
...
·
|
|---|
An added difficulty would probably also be that you would need to solve the equations per pixel (at least for ha and SII), since the intensity for each line is a function of the spatial coordinates and we cannot expect that the ratios of them are constant.
|
0.90
...
·
|
|---|
Please correct me if I've got it wrong, but can this really be solved mathematically? You don't know how much of the red signal, for example, comes through Ha or Sii? That is, even if I know what the filter's transmission is at the corresponding points, I don't know whether I really recorded any Sii signal, for example? Assuming I photograph an area in which there is no Sii. If I apply any formulas to it, I would create an Sii image from it, even though there is no Sii in the region? |
19.05
...
·
·
2
likes
|
|---|
You cannot split the Ha and Sii signal via this method. Konrad is correct. Worse yiu dont kniw how much continuum is being added from the extreme blue window and deep red windows. That cannot be split either. Best to just think of tge quad band filter as an extreme light pollution filter |
