I am looking at getting new 50mm narrowband filters. I was looking at Chroma Ha 5nm vs 3nm filters. Cost is not an issue, but I have read on multiple occasions that the 3nm filters will miss the NII bandpass details in certain planetary nebulae.
Does anyone have any examples of NII signals that can go missing in the 3nm filters? How significant is it?
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Here’s a comparison done quite a while back by Frank over at CloudyNights: https://www.cloudynights.com/topic/448214-5nm-ha-or-3nm-hanii-what-is-best/?p=5805605M27 and M57 are quite rich in NII, so the difference is noticeable. The other consideration is galaxies with a heavy red shift. If you’re trying to capture Ha regions in distant galaxies, a wider bandpass may be of benefit. On the other hand, the narrower bandpass will help maximise SNR pretty much everywhere else.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Which one of the two NII lines? Otherwise you can help yourself with some NB spectra such as: M27: 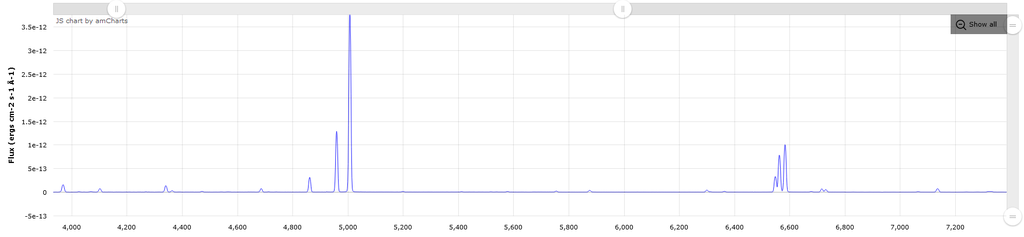 In some cases you loose more from ignoring Hb than by ignoring the NII lines. Link to some PN spectra: https://web.williams.edu/Astronomy/research/PN/nebulae/search/index.php |
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Thanks those are great links!
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Aaron H.:
Here’s a comparison done quite a while back by Frank over at CloudyNights:
https://www.cloudynights.com/topic/448214-5nm-ha-or-3nm-hanii-what-is-best/?p=5805605
M27 and M57 are quite rich in NII, so the difference is noticeable.
The other consideration is galaxies with a heavy red shift. If you’re trying to capture Ha regions in distant galaxies, a wider bandpass may be of benefit. How distant do the galaxies need to be be before the redshif is significant enough to move the Ha out of the 3nm band? I don't think I tried to capture Ha on galaxies farther than 100m light years away.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Ashraf AbuSara:
Aaron H.:
Here’s a comparison done quite a while back by Frank over at CloudyNights:
https://www.cloudynights.com/topic/448214-5nm-ha-or-3nm-hanii-what-is-best/?p=5805605
M27 and M57 are quite rich in NII, so the difference is noticeable.
The other consideration is galaxies with a heavy red shift. If you’re trying to capture Ha regions in distant galaxies, a wider bandpass may be of benefit.
How distant do the galaxies need to be be before the redshif is significant enough to move the Ha out of the 3nm band? I don't think I tried to capture Ha on galaxies farther than 100m light years away. Assuming 656 nm will be observed at 657 nm (meaning a 1 nm shift), the redshift (z) value is z=0.0015. That roughly corresponds to a luminosity distance of 30 Mly.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
Ashraf AbuSara:
Aaron H.:
Here’s a comparison done quite a while back by Frank over at CloudyNights:
https://www.cloudynights.com/topic/448214-5nm-ha-or-3nm-hanii-what-is-best/?p=5805605
M27 and M57 are quite rich in NII, so the difference is noticeable.
The other consideration is galaxies with a heavy red shift. If you’re trying to capture Ha regions in distant galaxies, a wider bandpass may be of benefit.
How distant do the galaxies need to be be before the redshif is significant enough to move the Ha out of the 3nm band? I don't think I tried to capture Ha on galaxies farther than 100m light years away.
Assuming 656 nm will be observed at 657 nm (meaning a 1 nm shift), the redshift (z) value is z=0.0015. That roughly corresponds to a luminosity distance of 30 Mly. Thank you for the math Kay. So looking at the Chroma Ha 3nm filter, it looks like it will transmit more than 90% of the signal upto 658nm. https://www.chroma.com/products/parts/27001-h-alpha-3nm-bandpass |
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Ashraf AbuSara:
Thank you for the math Kay. So looking at the Chroma Ha 3nm filter, it looks like it will transmit more than 90% of the signal upto 658nm.
https://www.chroma.com/products/parts/27001-h-alpha-3nm-bandpass I shan't think so, it's more like ~0.47%. OTOH, NII, like all ionized (with more than one proton) atoms has two resonant emission lines, the one most prominent is the one at 658.4 nm (the other one is @ 654.8 nm). So that filter won't cover more than 16% of NII at the longer wavelength and ~31% at the shorter wavelength.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
andrea tasselli:
Ashraf AbuSara:
Thank you for the math Kay. So looking at the Chroma Ha 3nm filter, it looks like it will transmit more than 90% of the signal upto 658nm.
https://www.chroma.com/products/parts/27001-h-alpha-3nm-bandpass
I shan't think so, it's more like ~0.47%. OTOH, NII, like all ionized (with more than one proton) atoms has two resonant emission lines, the one most prominent is the one at 658.4 nm (the other one is @ 654.8 nm). So that filter won't cover more than 16% of NII at the longer wavelength and ~31% at the shorter wavelength. Oh I knew it did not pass the Nii emission wavelength. That I understand. I am following up on the question of how distant a galaxy needs to be before the Ha signal suffers from a red shift significant enough that it can no longer come through the filter.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
Assuming 656 nm will be observed at 657 nm (meaning a 1 nm shift), the redshift (z) value is z=0.0015. That roughly corresponds to a luminosity distance of 30 Mly. Since the redshift values are actually derived from a curve fit over very large distances, you'd have to be careful in using Hubble's law to derive the actual redshift of relatively close by galaxies such as those at distances of 30 Mly, generally the types of galaxies we image. For any galaxy you want to image, I'd think it would be easier to actually find the redshift value from literature. As an example, M101, about 20 Mly away, has a redshift value of 0.000804. The scale of distances over which the linear fit is done to derive Hubble's constant is enormously larger than the distances of galaxies we typically image. 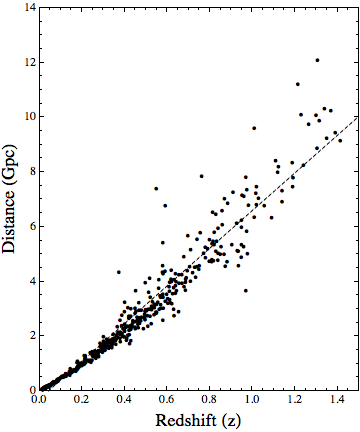 |
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Ashraf AbuSara:
Oh I knew it did not pass the Nii emission wavelength. That I understand.
I am following up on the question of how distant a galaxy needs to be before the Ha signal suffers from a red shift significant enough that it can no longer come through the filter. *In that case the Ha ceases to be observable with that specific filter for a z value > of 2/656.3 = 0.003047, from which one can derive the distance (in megapersec, Mpc) knowing the Hubble constant (Ho ~ 71 (km/s)/Mpc) and the relation Distance = z*c/Ho (where c is the speed of light in void). That is roughly 13 Mpc or 42 Mly.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Hmmm I might stick to the 5nm filter then. Might suffer slightly more with a bright moon. I want to be able to capture the Ha data on galaxies upto 100m Ly away.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Arun H:
Kay Ogetay:
Assuming 656 nm will be observed at 657 nm (meaning a 1 nm shift), the redshift (z) value is z=0.0015. That roughly corresponds to a luminosity distance of 30 Mly.
Since the redshift values are actually derived from a curve fit over very large distances, you'd have to be careful in using Hubble's law to derive the actual redshift of relatively close by galaxies such as those at distances of 30 Mly, generally the types of galaxies we image. For any galaxy you want to image, I'd think it would be easier to actually find the redshift value from literature. As an example, M101, about 20 Mly away, has a redshift value of 0.000804. The scale of distances over which the linear fit is done to derive Hubble's constant is enormously larger than the distances of galaxies we typically image.
 Redshift value is not derived, it is the measured parameter. Distance is derived from the redshift (in particular, the luminosity distance I'm referring to). Basically the calculation I made is as follows: Calculate the z-value of a shift for actual wavelength 656nm and observed wavelength 657nm. Which gives us approximately z=0.0015. Then the part where we convert redshift (z) to luminosity distance is a bit tricky because it involves factors such as the Hubble parameter and the geometry of the universe. For flat universe and H_0 approximately 70, I got the result of approximately 30 Mly. I believe you went the other way around, please correct me if I misunderstood you.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
Redshift value is not derived, it is the measured parameter. Distance is derived from the redshift (in particular, the luminosity distance I'm referring to). Basically the calculation I made is as follows:
Calculate the z-value of a shift for actual wavelength 656nm and observed wavelength 657nm. Which gives us approximately z=0.0015. Then the part where we convert redshift (z) to luminosity distance is a bit tricky because it involves factors such as the Hubble parameter and the geometry of the universe. For flat universe and H_0 approximately 70, I got the result of approximately 30 Mly. I believe you went the other way around, please correct me if I misunderstood you. I should have been more clear in what I said. Yes, redshift values are measured, for individual galaxies. But a plot of distance versus redshift is used to derive, for example, Hubble's constant. Knowing Hubble's constant and, neglecting for simplicity things like curvature, you could estimate the redshift of a theoretical galaxy at some specified distance. But the actual redshift of a galaxy can vary from this estimate as seen from the scatter in the graph and, for small distances, this variance could be significant. So my point was that, especially for small distances, redshift estimates based on distance alone can have error associated with them, and that error may be significant. So, especially for close galaxies where the actual redshift is known quite accurately, it may be better to use that to determine whether the redshift of that galaxy is large enough or not to capture the H-alpha using a narrowband filter.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
I might just stick my Chroma 3nm Ha filter tonight on C44, and then perform a continuum subtraction on the red channel from data I collected in the past or when the moon is lower, see if I got anything at all.
I can't find a single example of this target in HaLRGB.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Arun H:
Kay Ogetay:
Redshift value is not derived, it is the measured parameter. Distance is derived from the redshift (in particular, the luminosity distance I'm referring to). Basically the calculation I made is as follows:
Calculate the z-value of a shift for actual wavelength 656nm and observed wavelength 657nm. Which gives us approximately z=0.0015. Then the part where we convert redshift (z) to luminosity distance is a bit tricky because it involves factors such as the Hubble parameter and the geometry of the universe. For flat universe and H_0 approximately 70, I got the result of approximately 30 Mly. I believe you went the other way around, please correct me if I misunderstood you.
I should have been more clear in what I said.
Yes, redshift values are measured, for individual galaxies.
But a plot of distance versus redshift is used to derive, for example, Hubble's constant.
Knowing Hubble's constant and, neglecting for simplicity things like curvature, you could estimate the redshift of a theoretical galaxy at some specified distance. But the actual redshift of a galaxy can vary from this estimate as seen from the scatter in the graph and, for small distances, this variance could be significant.
So my point was that, especially for small distances, redshift estimates based on distance alone can have error associated with them, and that error may be significant. So, especially for close galaxies where the actual redshift is known quite accurately, it may be better to use that to determine whether the redshift of that galaxy is large enough or not to capture the H-alpha using a narrowband filter. I'm sorry, still not clear to me how this relates to my answer. If you are saying, use observed z-values of individual galaxies rather than calculate, yes. What I calculated was to find what z-values are out of the filter's bandwidth. Then I calculated (separately) what that z-values corresponded to in terms of luminosity distance (using the Hubble parameter and the curvature). Also, our z values are too small for such significant errors, one can use Andrea's linear equation as well. The deviation (as the plot you attached also shows) starts for a higher z that we do not observe. If we care about details, a more important one comes from the F-ratio and filter relation as it will shift the peak transmission as well. In practice there are so many factors, so I prefer to do a rough calculation to determine the threshold. Ashraf AbuSara:
Hmmm I might stick to the 5nm filter then. Might suffer slightly more with a bright moon. I want to be able to capture the Ha data on galaxies upto 100m Ly away. I believe Ashraf got the intuition he was looking for. Which I thought in the past as well. I'd go with the 5nm under very dark skies, if I'm not chasing extremely faint Ha emissions. For galaxies and PNs, I'd go for 5nm. In fact, if I'm buying cheap Ha filter, then I'd go with 5nm just to be safe as well. Not sure about the recent updates, but some were deviating significantly from the peak transmission line. I remember the inconsistency between the same filters. They provide the transmission sheet now, but who actually verifies it?
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Ashraf AbuSara:
Hmmm I might stick to the 5nm filter then. Might suffer slightly more with a bright moon. I want to be able to capture the Ha data on galaxies upto 100m Ly away.
I believe Ashraf got the intuition he was looking for. Which I thought in the past as well. I'd go with the 5nm under very dark skies, if I'm not chasing extremely faint Ha emissions. For galaxies and PNs, I'd go for 5nm.
In fact, if I'm buying cheap Ha filter, then I'd go with 5nm just to be safe as well. Not sure about the recent updates, but some were deviating significantly from the peak transmission line. I remember the inconsistency between the same filters. They provide the transmission sheet now, but who actually verifies it?
Thanks Kay. Great discussion! I ordered Ha 5nm filter. I have a 36mm 3nm filter too. I might do a head to head. Maybe some real life experimentation will shed some light on their limitations.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
Then I calculated (separately) what that z-values corresponded to in terms of luminosity distance (using the Hubble parameter and the curvature). It is fine. The original poster seems happy with your answer. Debating further will not add value and will likely result in a long and ultimately not very useful thread. In any case, a 5 nm filter will, in general allow a broader range of galaxies to be measured. For others that are interested here is a reference. And an extract from the reference ( https://www.e-education.psu.edu/astro801/content/l10_p3.html): There are a couple of important caveats that apply to Hubble's Law. They are:
- Hubble's Law only works for distant galaxies. For nearby galaxies (in the Local Group), stars inside the Milky Way, and for objects in our Solar System, the relationship between distance and velocity does not hold. The reason for the discrepancy for nearby galaxies is the "peculiar velocity" of the galaxy, that is, its real velocity through space that is unrelated to the expansion. For distant galaxies, their peculiar velocities are small enough that they still lie on or near the line for Hubble's Law. For nearby galaxies, though, their peculiar velocity is larger than their velocity from the expansion, so their peculiar velocity dominates their total velocity, causing them to lie far from the line relating velocity to distance. For example, the galaxy M31 does not even show a redshift; it is blueshifted, showing that its peculiar velocity is pointed towards us, rather than away from us.
Calculating Luminosity distance for close galaxies from Hubble's law will be prone to error because factors other than expansion are more important.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Arun H:
Kay Ogetay:
Then I calculated (separately) what that z-values corresponded to in terms of luminosity distance (using the Hubble parameter and the curvature).
It is fine.
The original poster seems happy with your answer. Debating further will not add value and will likely result in a long and ultimately not very useful thread.
In any case, a 5 nm filter will, in general allow a broader range of galaxies to be measured.
For others that are interested here is a reference. And an extract from the reference (https://www.e-education.psu.edu/astro801/content/l10_p3.html):
There are a couple of important caveats that apply to Hubble's Law. They are:
- Hubble's Law only works for distant galaxies. For nearby galaxies (in the Local Group), stars inside the Milky Way, and for objects in our Solar System, the relationship between distance and velocity does not hold. The reason for the discrepancy for nearby galaxies is the "peculiar velocity" of the galaxy, that is, its real velocity through space that is unrelated to the expansion. For distant galaxies, their peculiar velocities are small enough that they still lie on or near the line for Hubble's Law. For nearby galaxies, though, their peculiar velocity is larger than their velocity from the expansion, so their peculiar velocity dominates their total velocity, causing them to lie far from the line relating velocity to distance. For example, the galaxy M31 does not even show a redshift; it is blueshifted, showing that its peculiar velocity is pointed towards us, rather than away from us.
Calculating Luminosity distance for close galaxies from Hubble's law will be prone to error because factors other than expansion are more important. Oh now I see what you are referring to, thanks. You are referring to the "peculiar motions of galaxies in our neighborhood". My goal was not to calculate distance from the redshift. As Ashraf asked, I calculated the "maximum effective distance that a filter can see". Indeed these galaxies' peculiar velocity is more dominant than the speed caused by the Hubble expansion. I'm not aware of their z-value distribution but from the ones that I know, Andromeda is z=-0.001 is still smaller than this threshold. Now I quickly looked up M33 is -0.0006 even smaller. I'm assuming all will fall below the calculated z-range anyway, unless there are some speedy ones that I'm not aware.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
Indeed these galaxies' peculiar velocity is more dominant than the speed caused by the Hubble expansion. I'm not aware of their z-value distribution but from the ones that I know, Andromeda is z=-0.001 is still smaller than this threshold. Now I quickly looked up M33 is -0.0006 even smaller. I'm assuming all will fall below the calculated z-range anyway, unless there are some speedy ones that I'm not aware. Yes, I guess my point was - the galaxies we typically image have small redshifts comparatively. In my way of thinking, it would be almost better to have a table of galaxies with actual observed redshifts (which are mostly dictated by peculiar motion rather than large scale Hubble expansion) and see which ones would have significant drops from a 3nm vs 5 nm filter. You are always going to be better off with a 5nm filter for this kind of thing, but how many of the galaxies you want to image can still be reasonably done with a 3nm filter, if you want to take advantage of the extra contrast that you get with that for nebula imaging?
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Arun H:
Kay Ogetay:
Indeed these galaxies' peculiar velocity is more dominant than the speed caused by the Hubble expansion. I'm not aware of their z-value distribution but from the ones that I know, Andromeda is z=-0.001 is still smaller than this threshold. Now I quickly looked up M33 is -0.0006 even smaller. I'm assuming all will fall below the calculated z-range anyway, unless there are some speedy ones that I'm not aware.
Yes, I guess my point was - the galaxies we typically image have small redshifts comparatively. In my way of thinking, it would be almost better to have a table of galaxies with actual observed redshifts (which are mostly dictated by peculiar motion rather than large scale Hubble expansion) and see which ones would have significant drops from a 3nm vs 5 nm filter. You are always going to be better off with a 5nm filter for this kind of thing, but how many of the galaxies you want to image can still be reasonably done with a 3nm filter, if you want to take advantage of the extra contrast that you get with that for nebula imaging? That's a pretty good question. And I don't think the answer would be rigorous, but would rather be a personal choice. I'd go with 5nm, because of many factors to be safe, if I'm going after such galaxy imaging, under a dark sky. I have seen some comparisons enough for me to forget about that contrast. You can always expose more to get more contrast, but if the emission line is outside of your filter's range, there is nothing you can do.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.
Kay Ogetay:
I have seen some comparisons enough for me to forget about that contrast. I also agree that, under a dark sky, a 5 nm makes more sense. H-alpha is almost always by far the strongest line and hence more forgiving the whatever effects of background pollution there may be.
|
You cannot like this item. Reason: "ANONYMOUS".
You cannot remove your like from this item.
Editing a post is only allowed within 24 hours after creating it.
You cannot Like this post because the topic is closed.
Copy the URL below to share a direct link to this post.
This post cannot be edited using the classic forums editor.
To edit this post, please enable the "New forums experience" in your settings.




